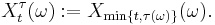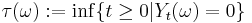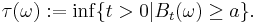Stopped process

In mathematics, a stopped process is a stochastic process that is forced to assume the same value after a prescribed (possibly random) time.

1 Definition
2 Examples
- 2.1 Gambling
- 2.2 Brownian motion
3 See also

Definition

Let

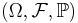$(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space;
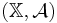$(\mathbb{X}, \mathcal{A})$ be a measurable space;
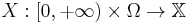$X�: [0, %2B \infty) \times \Omega \to \mathbb{X}$ be a stochastic process;
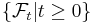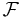$\tau�: \Omega \to [0, %2B \infty]$ be a stopping time with respect to some filtration $\{ \mathcal{F}_{t} | t \geq 0 \}$ of ${}\mathcal{F}$ .

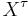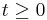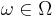Then the stopped process $X^{\tau}$ is defined for $t \geq 0$ and $\omega \in \Omega$ by

$X_{t}^{\tau} (\omega)�:= X_{\min \{ t, \tau (\omega) \}} (\omega).$

Examples

Gambling

Consider a gambler playing roulette. X_t denotes the gambler's total holdings in the casino at time t ≥ 0, which may or may not be allowed to be negative, depending on whether or not the casino offers credit. Let Y_t denote what the gambler's holdings would be if he/she could obtain unlimited credit (so Y can attain negative values).

Stopping at a deterministic time: suppose that the casino is prepared to lend the gambler unlimited credit, and that the gambler resolves to leave the game at a predetermined time T, regardless of the state of play. Then X is really the stopped process Y^T, since the gambler's account remains in the same state after leaving the game as it was in at the moment that the gambler left the game.

Stopping at a random time: suppose that the gambler has no other sources of revenue, and that the casino will not extend its customers credit. The gambler resolves to play until and unless he/she goes broke. Then the random time

$\tau (\omega)�:= \inf \{ t \geq 0 | Y_{t} (\omega) = 0 \}$

is a stopping time for Y, and, since the gambler cannot continue to play after he/she has exhausted his/her resources, X is the stopped process Y^τ.

Brownian motion

Let 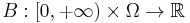$B�: [0, %2B \infty) \times \Omega \to \mathbb{R}$ be a one-dimensional standard Brownian motion starting at zero.

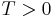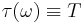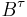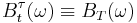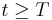Stopping at a deterministic time $T > 0$ : if $\tau (\omega) \equiv T$ , then the stopped Brownian motion $B^{\tau}$ will evolve as per usual up until time $T$ , and thereafter will stay constant: i.e., $B_{t}^{\tau} (\omega) \equiv B_{T} (\omega)$ for all $t \geq T$ .

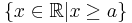Stopping at a random time: define a random stopping time $\tau$ by the first hitting time for the region $\{ x \in \mathbb{R} | x \geq a \}$ :

$\tau (\omega)�:= \inf \{ t > 0 | B_{t} (\omega) \geq a \}.$

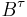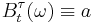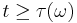Then the stopped Brownian motion $B^{\tau}$ will evolve as per usual up until the random time $\tau$ , and will thereafter be constant with value $a$ : i.e., $B_{t}^{\tau} (\omega) \equiv a$ for all $t \geq \tau (\omega)$ .

Stopped process

Contents

Definition

Examples

Gambling

Brownian motion

See also